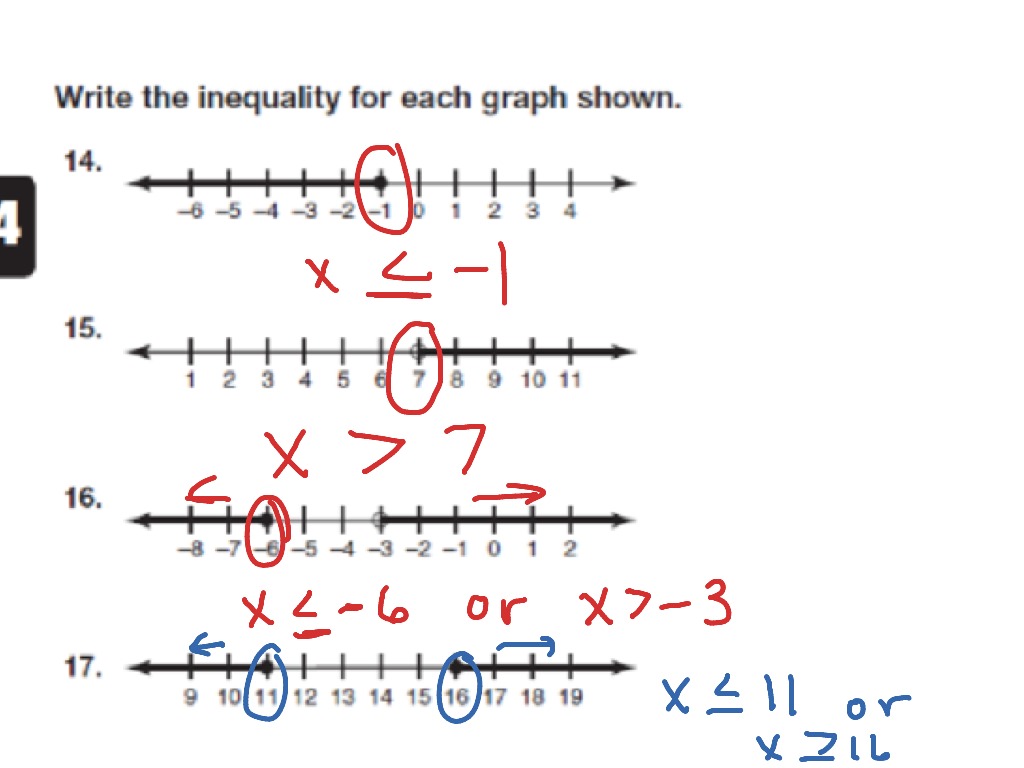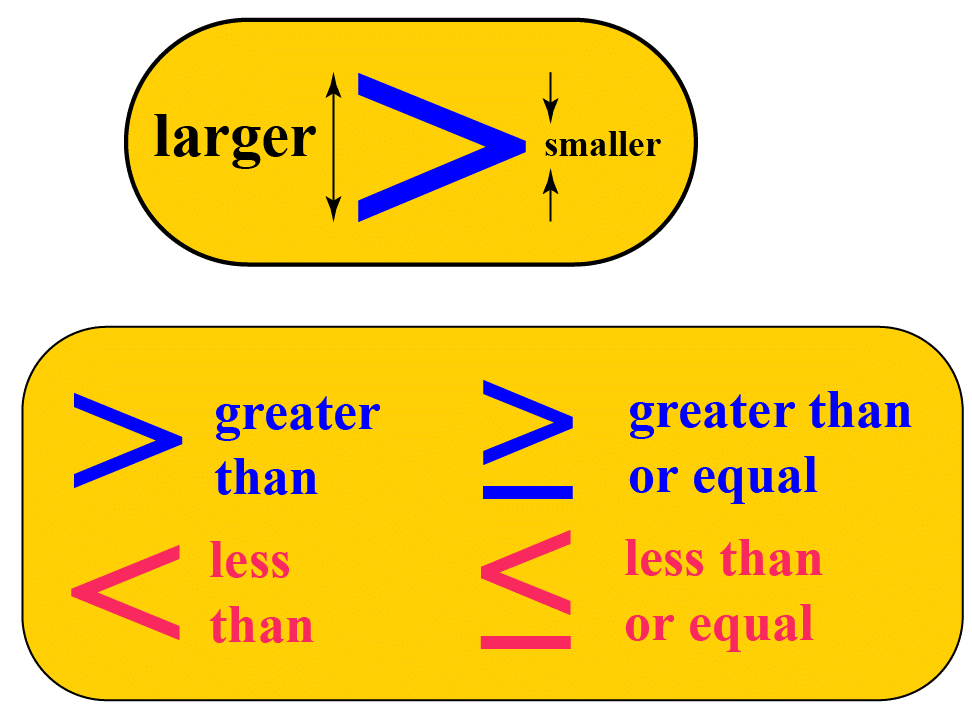Fantastic Tips About How To Learn Inequalities

Lifelong learning is a powerful tool that can equip individuals with the skills and knowledge needed to foster societies which are inclusive of all genders.

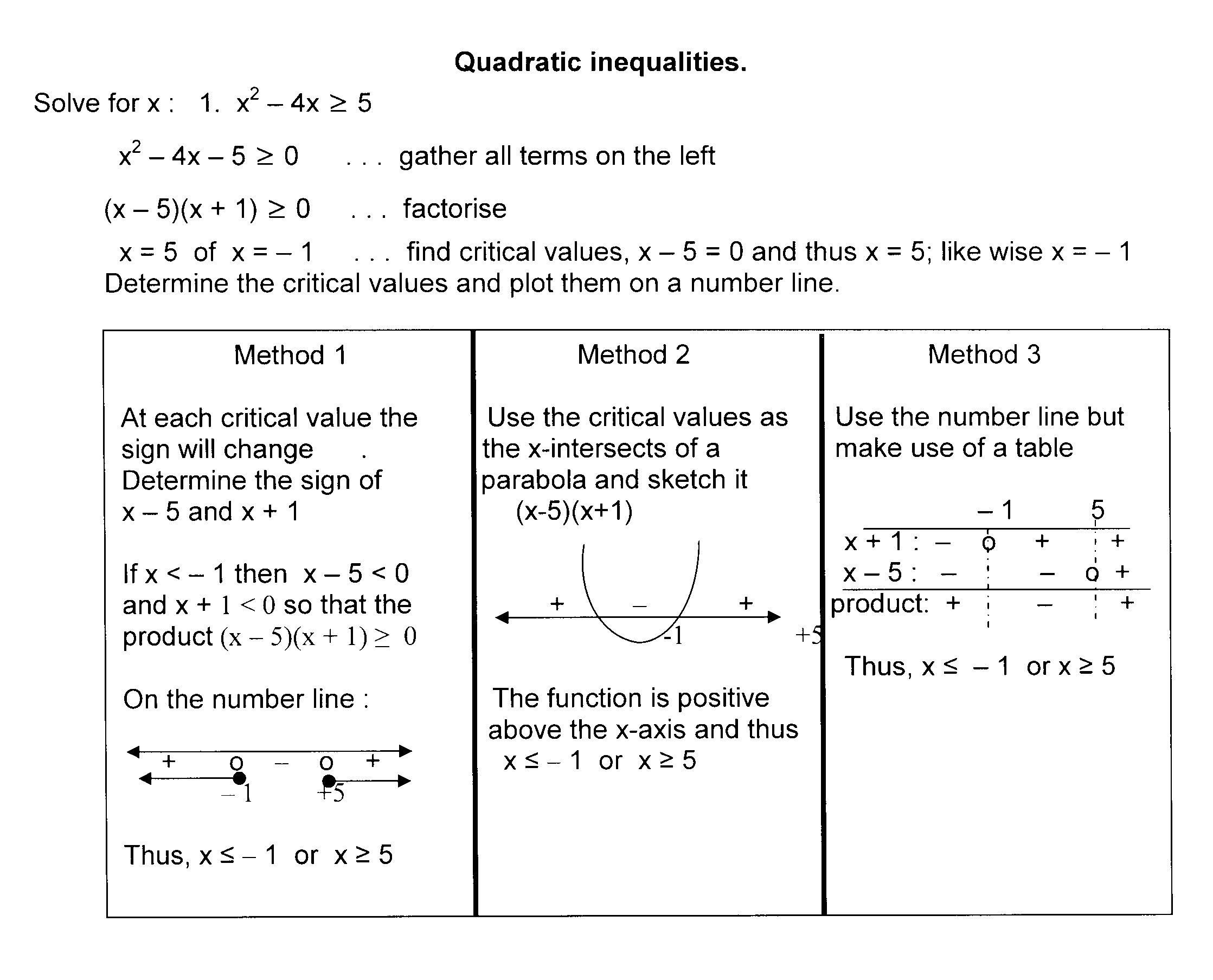
How to learn inequalities. Sometimes we need to solve inequalities like these: You must be 13 or older to watch a movie. In an equality, the value of x x can be many numbers.

Solving inequalities and solving equations Apply the distributive property to remove the parentheses. In this unit, we'll learn how to check your work, spot errors, and use key properties to simplify and solve problems.

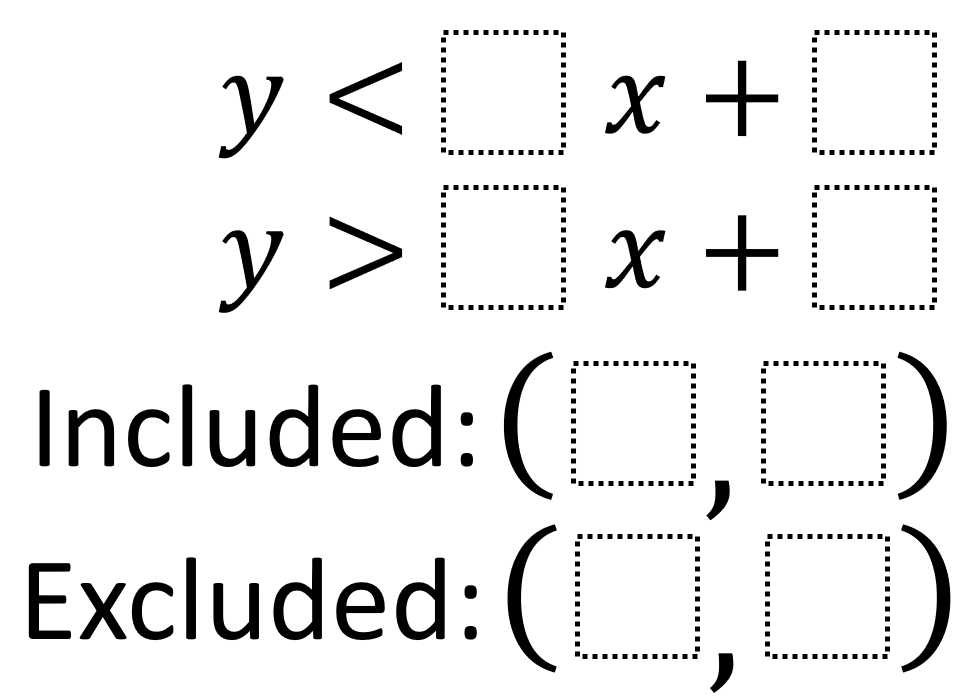
We can also have inequalities that include equals, like: You can represent inequalities on a number line. We'll also see what it takes for an equation to have no solution, or infinite solutions.

Learn about and revise how to show inequalities on number lines and graphs, as well as solve inequalities with this bbc bitesize gcse maths edexcel guide. Recall, that x = 5 x = 5 is an equation. In the following guide, you will learn more about linear inequality and solving it.

Greater than sign less than or equal to e.g. Knowing how to solve them is a basic math skill used in nearly every academic discipline and in many jobs. The inequality is between your age and the age of 13.

In mathematics, inequality represents the mathematical expression in which both. Age ≥ 13 comparing values practice >, < and = with compare numbers to 10 Solutions can be integers or decimals, positive or negative numbers.

X + 2 > 12 subtract 2 from both sides: What is linear inequality in maths? Let's explore some different ways to solve equations and inequalities.

Solving inequalities, systems of inequalities. Nonlinear bayesian optimal experimental design using logarithmic sobolev inequalities.

Yet unesco data shows that 40 per cent of the world’s population does not have access to an. 11 years ago when sal shows that no matter what x is, y is always going to be greater than 5, how can you tell why he knows :? We study the problem of selecting experiments from a larger candidate pool, where the goal is to maximize mutual information (mi) between the selected subset and the underlying parameters.

We will now equate two algebraic expressions and think about how it might constrain what value the variables can take on. How to solve inequalities solving an inequality by adding/subtracting numbers on both sides of the inequality or by multiplying/dividing both. To do this we need to balance the inequality in the same way as we would when solving an equation.